Partial cube

In graph theory, a partial cube is a graph that is an isometric subgraph of a hypercube. In other words, a partial cube is a subgraph of a hypercube that preserves distances—the distance between any two vertices in the subgraph is the same as the distance between those vertices in the hypercube. Equivalently, a partial cube is a graph whose vertices can be labeled with bit strings of equal length in such a way that the distance between two vertices in the graph is equal to the Hamming distance between their labels. Such a labeling is called a Hamming labeling; it represents an isometric embedding of the partial cube into a hypercube.

1 Examples
2 Recognition
3 The Djoković–Winkler relation
4 Application to chemical graph theory
5 Notes
6 References

Examples

The Desargues graph is a partial cube, as is more generally any bipartite Kneser graph H_2n+1,n. In this bipartite Kneser graph, the labels consist of all possible (2n + 1)-digit bitstrings that have either n or n + 1 nonzero bits; the Desargues graph is constructed in this way with n = 2.

All median graphs are partial cubes. Since the median graphs include the squaregraphs, simplex graphs, and Fibonacci cubes, as well as the covering graphs of finite distributive lattices, these are all partial cubes. The planar dual graph of an arrangement of lines in the Euclidean plane, is a partial cube; more generally, for any hyperplane arrangement in Euclidean space of any number of dimensions, the graph that has a vertex for each cell of the arrangement and an edge for each two adjacent cells is a partial cube.

A partial cube in which every vertex has exactly three neighbors is known as a cubic partial cube. Although several infinite families of cubic partial cubes are known, together with many other sporadic examples, the only known cubic partial cube that is not a planar graph is the Desargues graph.^[1]

The underlying graph of any antimatroid, having a vertex for each set in the antimatroid and an edge for every two sets that differ by a single element, is always a partial cube.

Recognition

Partial cubes can be recognized, and a Hamming labeling constructed, in 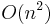$O(n^2)$ time, where $n$ is the number of vertices in the graph.^[2]

The Djoković–Winkler relation

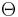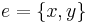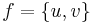Many of the theorems about partial cubes, including the recognition algorithm mentioned above, are based directly or indirectly upon a certain binary relation defined on the edges of the graph. This relation, first described by Djoković (1973) and given an equivalent definition in terms of distances by Winkler (1984), is denoted by $\Theta$ . 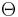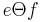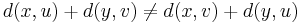Two edges $e=\{x,y\}$ and $f=\{u,v\}$ are defined to be in the relation $\Theta$ , written $e\mathrel{\Theta}f$ , if $d(x,u)%2Bd(y,v)\not=d(x,v)%2Bd(y,u)$ . This relation is reflexive and symmetric, but in general it is not transitive.

Winkler showed that a connected graph is a partial cube if and only if it is bipartite and the relation 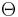$\Theta$ is transitive.^[3] In this case, it forms an equivalence relation and each equivalence class separates two connected subgraphs of the graph from each other. A Hamming labeling may be obtained by assigning one bit of each label to each of the equivalence classes of the Djoković–Winkler relation; in one of the two connected subgraphs separated by an equivalence class of edges, all of the vertices have a 0 in that position of their labels, and in the other connected subgraph all of the vertices have a 1 in the same position.

Application to chemical graph theory

Isometric embeddings of graphs into hypercubes have an important application in chemical graph theory. A benzenoid graph is a graph consisting of all vertices and edges lying on and in the interior of a cycle in a hexagonal lattice. Such graphs are the molecular graphs of the benzenoid hydrocarbons, a large class of organic molecules. Every such graph is a partial cube.^[4] A Hamming labeling of such a graph can be used to compute the Wiener index of the corresponding molecule,^[5] which can then be used to predict certain of its chemical properties.

A different molecular structure formed from carbon, the diamond cubic, also forms partial cube graphs.^[6]

Notes

^ Eppstein (2006).
^ Eppstein (2008).
^ Winkler (1984), Theorem 4.
^ Klavžar, Gutman & Mohar (1995), Theorem 2.1; Imrich & Klavžar (2000), Proposition 2.13, p. 60.
^ Klavžar, Gutman & Mohar (1995), Proposition 3.1; Imrich & Klavžar (2000), Proposition 2.14, p. 60.
^ Eppstein (2009).

References

Djoković, D. Ž. (1973), "Distance-preserving subgraphs of hypercubes", Journal of Combinatorial Theory, Series B 14 (3): 263–267, doi:10.1016/0095-8956(73)90010-5, MR 0314669 .
Eppstein, David (2006), "Cubic partial cubes from simplicial arrangements", Electronic J. Combinatorics 13 (1): #R79, arXiv:math.CO/0510263, http://www.combinatorics.org/Volume_13/Abstracts/v13i1r79.html .
Eppstein, David (2008), "Recognizing partial cubes in quadratic time", Proc. 19th ACM-SIAM Symposium on Discrete Algorithms, pp. 1258–1266, arXiv:0705.1025 .
Eppstein, David (2009), "Isometric diamond subgraphs", Proc. 16th International Symposium on Graph Drawing, Heraklion, Crete, 2008, Lecture Notes in Computer Science, 5417, Springer-Verlag, pp. 384–389, arXiv:0807.2218, doi:10.1007/978-3-642-00219-9_37 .
Imrich, Wilfried; Klavžar, Sandi (2000), Product Graphs: Structure and Recognition, Wiley-Interscience Series in Discrete Mathematics and Optimization, New York: John Wiley & Sons, ISBN 978-0-471-37039-0, MR 1788124 .
Klavžar, Sandi; Gutman, Ivan; Mohar, Bojan (1995), "Labeling of benzenoid systems which reflects the vertex-distance relations", Journal of Chemical Information and Computer Sciences 35 (3): 590–593 .
Winkler, Peter M. (1984), "Isometric embedding in products of complete graphs", Discrete Applied Mathematics 7 (2): 221–225, doi:10.1016/0166-218X(84)90069-6, MR 0727925 .